РАЗМЫШЛЕНИЯ О ТЕОРЕМЕ ФЕРМА
Напрасно
пытаться сделать посредством большего то,
что может
быть сделано посредством меньшего.
Оккама
Вступление.
Господа! Предлагаю вам перечень
найденных мною решений математических вопросов:
1. Доказательство Теоремы Ферма на
основании того факта, что уравнения ![]() и
и ![]() идентичны
(преобразовываются одно в другое). Это
позволяет утверждать, что в уравнении
идентичны
(преобразовываются одно в другое). Это
позволяет утверждать, что в уравнении ![]() , при n – целом числе >2 одна из переменных
(x; y;
z) должна равняться Б
(бесконечной периодической дроби). Причем избавиться от этой бесконечной
непериодической дроби невозможно.
, при n – целом числе >2 одна из переменных
(x; y;
z) должна равняться Б
(бесконечной периодической дроби). Причем избавиться от этой бесконечной
непериодической дроби невозможно.
На возможность подобного решения
указывается в одном из номеров «Техники молодежи» (примерно 1980), где
утверждается, что теорема Ферма справедлива, потому что справедливо уравнение ![]() , - правда, без основания этого утверждения. Поэтому в данном
решении нет ничего нового (!?).
, - правда, без основания этого утверждения. Поэтому в данном
решении нет ничего нового (!?).
Учитывая этот вопрос, я пошел дальше
и решил проблему «в целом»: при каких
значениях ![]() уравнение
уравнение ![]() может иметь целочисленные по x; y;
z решения?
может иметь целочисленные по x; y;
z решения?
2.Это решение можно сформулировать
так: уравнение ![]() , являясь уравнением четырех переменных (x; y;
z; n)
при
, являясь уравнением четырех переменных (x; y;
z; n)
при ![]() , может иметь целочисленные по всем четырем переменным
решения только при n=1 или 2. Во всех остальных случаях (
, может иметь целочисленные по всем четырем переменным
решения только при n=1 или 2. Во всех остальных случаях (![]() ) целочисленность
(конечность) любых трех их четырех переменных приводит значение четвертой к
равенству «Б» или бесконечности.
) целочисленность
(конечность) любых трех их четырех переменных приводит значение четвертой к
равенству «Б» или бесконечности.
Для доказательства этого решения
понадобилось:
2.1. показать возможность
геометрической интерпретации всех решений уравнения ![]() при
при
![]() в виде треугольника со
сторонами x; y;
z.
в виде треугольника со
сторонами x; y;
z.
2.2. Рассмотреть кривые, являющиеся
геометрическим местом (![]() ) вершин этих треугольников при фиксированном (const) значении «n» и стороны треугольника, лежащей
напротив этой вершины.
) вершин этих треугольников при фиксированном (const) значении «n» и стороны треугольника, лежащей
напротив этой вершины.
2.3. Показать «исключительность»
(родственность) этих кривых, заключающуюся в постоянстве (const) их кривизны на каждом их
участке при ![]() .
.
Описать способ решения на предмет их
(этих формул) целочисленности по x; y;
z при n>1.
2.4. Вывести с помощью этого способа
формулы для нахождения целочисленных по x; y;
z решений
уравнения ![]() как от одной
переменной (К), так и от двух (
как от одной
переменной (К), так и от двух (![]() ). Причем, эти формулы идентичны аналогичным формулам
Эвклида и Пифагора. Одновременный вывод этих формул говорит об их «родственности».
). Причем, эти формулы идентичны аналогичным формулам
Эвклида и Пифагора. Одновременный вывод этих формул говорит об их «родственности».
Сравните выведенные с помощью этого
способа тождества ![]() ;
; ![]() и формулы
Эвклида и Пифагора для нахождения
целочисленных решений квадратного уравнения
и формулы
Эвклида и Пифагора для нахождения
целочисленных решений квадратного уравнения ![]() .
.
Пифагор: ![]()
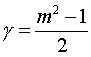 ;
; 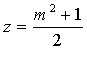 , где m – нечетное число.
, где m – нечетное число.
Эвклид: ![]() ;
; ![]() ;
; ![]() .
.
2.5. Показать взаимосвязь переменных
k и n , а на основании этого утверждать, что
обязательная конечность или бесконечная периодичность k приводит n к бесконечной непериодичности. Кроме этих вопросов, непосредственно
касающихся решения данной проблемы,
существуют и другие.
Основная часть.
Теорема Ферма гласит:
Уравнение вида xⁿ +
уⁿ = zⁿ , где n – целое положительное число, не имеет
целочисленных по х; у; z; решений
при n > 2.
Доказательство любой теоремы, в том числе и Теоремы Ферма, начинается с
установления её исходных данных, то есть с установления того, что нам Дано
и что требуется Доказать. Как ни
странно, именно это в формулировке автора (нарочно! или нет?) тщательно
завуалировано.*
Поэтому именно с этого и начнем. Предположим, что мы нашли решение уравнения
xⁿ +
уⁿ = zⁿ, в
котором: 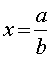 ;
;![]() ;
; 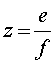 ; где
; где ![]() - целое число,
- целое число,
![]() - конечная дробь,
- конечная дробь, ![]() - бесконечная
периодическая дробь.
- бесконечная
периодическая дробь.
В этом случае мы можем избавиться и от конечности дроби, и от
бесконечной её периодичности, умножив уравнение xⁿ+уⁿ=zⁿ на их общий знаменатель (bdf)ⁿ.
Тогда получим: (adf)ⁿ+(cbf)ⁿ=(ebd)ⁿ,
где все числа (adf), (cbf), (ebd) - целые.
Единственно от чего мы не могли бы избавиться, это от бесконечной непериодической
дроби. Но отношение целых чисел не может равняться Б
(бесконечной непериодической дроби).
Следовательно, для выполнения Теоремы Ферма, в справедливости которой никто
не сомневается, необходимо записать:
Дано: Уравнение вида xⁿ+уⁿ=zⁿ , где n - целое положительное число.
Требуется Доказать, что х; у; z; могут принимать целочисленные (конечные) значения
только при n=1 и n=2; во всех остальных случаях (при n>2) одна из переменных (х;
у; z;)
должна равняться Б – бесконечной непериодической дроби.
Вспомним, что мы знаем о бесконечных непериодических дробях. Из школьной
программы всем известна формула для записи (описания) бесконечной непериодической
дроби: ![]() , где n – целое положительное
число. Вопрос заключается в установлении «пределов» её справедливости. То есть,
необходимо установить, при каких значениях а данная формула справедлива при
различных целых положительных значениях n.
, где n – целое положительное
число. Вопрос заключается в установлении «пределов» её справедливости. То есть,
необходимо установить, при каких значениях а данная формула справедлива при
различных целых положительных значениях n.
При n=1
данная формула не справедлива ни при каких целых конечных,
бесконечных
периодических значениях 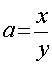 , где х и у – целые положительные
числа.
, где х и у – целые положительные
числа.
При n=2 данная
формула справедлива только при ![]() , равном целому
положительному числу. То есть, когда х = ау.
Но и в этом случае она содержит в себе гораздо больше информации, чем кажется
на первый взгляд.
, равном целому
положительному числу. То есть, когда х = ау.
Но и в этом случае она содержит в себе гораздо больше информации, чем кажется
на первый взгляд.
Разберемся на примере: ![]() , отсюда следует (на
первый взгляд), что
, отсюда следует (на
первый взгляд), что ![]() , то есть
, то есть ![]() .
.
Но ведь число 2 мы можем представить в виде дроби ![]() и т.д.
и т.д.
Тогда получаем: 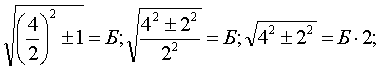 но 2Б всё равно остается Б (бесконечной не периодической дробью). Отсюда -
но 2Б всё равно остается Б (бесконечной не периодической дробью). Отсюда - ![]() . Подставляя значения
. Подставляя значения ![]() и т.д., мы получим
и т.д., мы получим ![]() и т.д. до
бесконечности.*
и т.д. до
бесконечности.*
При 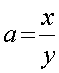 , где х, у - произвольные целые положительные
числа, не связанные зависимостью х=ау; (где а–целое
число) данная формула справедлива не всегда.
, где х, у - произвольные целые положительные
числа, не связанные зависимостью х=ау; (где а–целое
число) данная формула справедлива не всегда.
Например: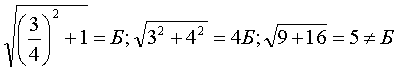 . Возможны и другие варианты.
. Возможны и другие варианты.
В дальнейшем будет показано, при каких значениях 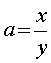 , данная формула не справедлива при n=2. Насколько мне было известно,
теория чисел указывает только комбинации чисел, кратных 3, 4, 5.** Однако,
набор этих чисел гораздо шире.
, данная формула не справедлива при n=2. Насколько мне было известно,
теория чисел указывает только комбинации чисел, кратных 3, 4, 5.** Однако,
набор этих чисел гораздо шире.
При n > 3 данная формула
справедлива при любых значениях 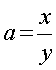 ; где х, у - целые положительные числа. Об этом нам
говорит Теорема Ферма. Ведь, подставив в уравнение
; где х, у - целые положительные числа. Об этом нам
говорит Теорема Ферма. Ведь, подставив в уравнение ![]() значение
значение 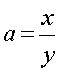 , получим:
, получим:
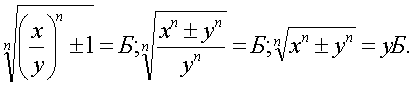
Обозначим у Б
буквой Z, учитывая, что Z - бесконечная непериодическая дробь. Тогда получим: ![]() , или
, или ![]() , где знак ± указывает, что в
уравнении, рассматриваемом в Теореме Ферма xⁿ + уⁿ = zⁿ, при n>3,
любая из переменных - х, у, z - может (и должна) равняться бесконечной
непериодической дроби, при условии конечности (целочисленности)
двух других. Таким образом, если границы применения формулы
, где знак ± указывает, что в
уравнении, рассматриваемом в Теореме Ферма xⁿ + уⁿ = zⁿ, при n>3,
любая из переменных - х, у, z - может (и должна) равняться бесконечной
непериодической дроби, при условии конечности (целочисленности)
двух других. Таким образом, если границы применения формулы ![]() ,
рассмотренные нами выше, оговорены и доказаны в теории чисел. Теорему Ферма
можно считать доказанной, так как она является следствием уравнения
,
рассмотренные нами выше, оговорены и доказаны в теории чисел. Теорему Ферма
можно считать доказанной, так как она является следствием уравнения![]() , где: при n = 2, а - целое число или строго определенные
простые дроби; при n
> 3, а - любое целое или дробное
число.*
, где: при n = 2, а - целое число или строго определенные
простые дроби; при n
> 3, а - любое целое или дробное
число.*
Если данные «границы» не оговорены и не доказаны, попытаемся установить
и обосновать их сами.
Как мы уже установили, уравнения ![]() и xⁿ+уⁿ=zⁿ взаимосвязаны и возможность
уравнения xⁿ +
уⁿ = zⁿ иметь конечные (целочисленные) по х; у; z;
решения определяет «границы» применения уравнения
и xⁿ+уⁿ=zⁿ взаимосвязаны и возможность
уравнения xⁿ +
уⁿ = zⁿ иметь конечные (целочисленные) по х; у; z;
решения определяет «границы» применения уравнения ![]() .
.
Поэтому поставим вопрос более «широко». Попытаемся определить (установить),
при каких значениях n в
интервале 1<n<![]() уравнение вида
уравнение вида
xⁿ +
уⁿ = zⁿ ; может
иметь целочисленные (конечные) по х; у; z; решения.
В дальнейшем, для краткости
изложения, будут освещены только основные (ключевые) моменты решения. Все
нюансы решайте самостоятельно (или смотрите приложение). Ибо только
самостоятельное их решение приводит к полному пониманию проблемы. Для большей наглядности
решаемой проблемы необходимо учесть, что любое решение уравнения xⁿ+уⁿ=zⁿ в интервалезначений
1<n<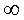 можно графически представить в виде
треугольника со сторонами х; у; z. Или, другими словами, любой треугольник является
графическим решением уравнения xⁿ+ уⁿ= zⁿ в интервале значений 1<n<
можно графически представить в виде
треугольника со сторонами х; у; z. Или, другими словами, любой треугольник является
графическим решением уравнения xⁿ+ уⁿ= zⁿ в интервале значений 1<n<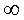 . Так как при n < 1 сумма x + y < z
и
. Так как при n < 1 сумма x + y < z
и 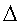 «разрывается».
«разрывается».
При n = 1 мы
получаем «критический» ![]() с углами, при вершинах равными 0°; 180°; 0°.
с углами, при вершинах равными 0°; 180°; 0°.

Решениям уравнения
при n =![]() соответствуют все равнобедренные
соответствуют все равнобедренные ![]() с углом между равными сторонами
с углом между равными сторонами ![]() < 60°. Остальные равнобедренные
< 60°. Остальные равнобедренные ![]() с углом 60°<
с углом 60°< ![]() <180° соответствуют решениям уравнения, когда х=у, то есть 2xⁿ=zⁿ. Но если
извлечь
<180° соответствуют решениям уравнения, когда х=у, то есть 2xⁿ=zⁿ. Но если
извлечь ![]() из этого уравнения,
получим
из этого уравнения,
получим ![]() . Учитывая, что
. Учитывая, что ![]() при
при 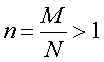 , где М, N - целые положительные числа, равняется Б, получаем, что либо x, либо z должны равняться Б.
Следовательно, все равнобедренные
, где М, N - целые положительные числа, равняется Б, получаем, что либо x, либо z должны равняться Б.
Следовательно, все равнобедренные ![]() с углом 60°<
с углом 60°<![]() <180° и целочисленными (конечными) значениями х; z; являются
решениями уравнения 2xⁿ=zⁿ , при n=Б.
<180° и целочисленными (конечными) значениями х; z; являются
решениями уравнения 2xⁿ=zⁿ , при n=Б.
Обобщая всё вышесказанное, можно сказать, что любой
равнобедренный![]() с конечными (целочисленными)
значениями сторон является графическим решением уравнения xⁿ+уⁿ=zⁿ при n=Б, или n=
с конечными (целочисленными)
значениями сторон является графическим решением уравнения xⁿ+уⁿ=zⁿ при n=Б, или n=![]() .* Для ещё большей наглядности построим и
рассмотрим кривые, являющиеся геометрическим местом (•) вершин
.* Для ещё большей наглядности построим и
рассмотрим кривые, являющиеся геометрическим местом (•) вершин ![]() , соответствующих решению уравнения xⁿ+уⁿ=zⁿ при различных фиксированных значениях 1<n<
, соответствующих решению уравнения xⁿ+уⁿ=zⁿ при различных фиксированных значениях 1<n<![]() и фиксированном значении одной из
сторон z, x или у. Причём, x или у достаточно,
ибо, фиксируя и x, и у, мы получим
одинаковые кривые. Собственно, для рассмотрения всех этих кривых достаточно
построить три «критические» кривые, соответствующие значениям n, равным 1; 2;
и фиксированном значении одной из
сторон z, x или у. Причём, x или у достаточно,
ибо, фиксируя и x, и у, мы получим
одинаковые кривые. Собственно, для рассмотрения всех этих кривых достаточно
построить три «критические» кривые, соответствующие значениям n, равным 1; 2;![]() .
.
1). При фиксированном
значении большей стороны (z) и n=1 мы получим отрезок прямой ______Z_______,
любая точка которого является решением
уравнения, х+у=z .

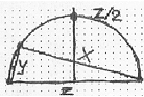
2). При фиксированном значении большей стороны (z) и n=2 мы
получим полуокружность радиусом z/2, каждая (•) из которой является вершиной ![]() со сторонами х; у; z; причём, левая
половина этой полуокружности до (•) z/2
соответствует решениям, когда х>у; правая - х< у; (•) z/2
соответствует х=у.
со сторонами х; у; z; причём, левая
половина этой полуокружности до (•) z/2
соответствует решениям, когда х>у; правая - х< у; (•) z/2
соответствует х=у.
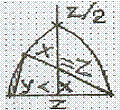
3). При фиксированном значении «большей» стороны (z) и n=![]() мы получим два отрезка окружности
радиуса z. Левый отрезок окружности до (•) z/2
соответствует решениям у<х = z, так как при z=
мы получим два отрезка окружности
радиуса z. Левый отрезок окружности до (•) z/2
соответствует решениям у<х = z, так как при z=![]() =1; z>y<1; 1>
=1; z>y<1; 1>![]() = 0; 0+1=1,
следовательно, х=1. (•) z/2
соответствует при z>1, z<1 решению х=у, ибо любое
число>1 в
= 0; 0+1=1,
следовательно, х=1. (•) z/2
соответствует при z>1, z<1 решению х=у, ибо любое
число>1 в![]() степени=
степени=![]() ; а
; а ![]() +
+![]() =
=![]() .
.
Любое число <1 в![]() степени = 0; 0+0=0. Единственное
исключение – это когда z = 1, х = у; тогда
степени = 0; 0+0=0. Единственное
исключение – это когда z = 1, х = у; тогда ![]() (так как
(так как ![]() = 1, а 1 + 1
= 1, а 1 + 1![]() 1); но в нашем случае этим можно пренебречьи
обсудить отдельно*. Правая часть окружности R=z
по аналогии соответствует решениям, когда х<у.
1); но в нашем случае этим можно пренебречьи
обсудить отдельно*. Правая часть окружности R=z
по аналогии соответствует решениям, когда х<у.
Теперь совместим эти три «критические» кривые в одном рисунке и получим:
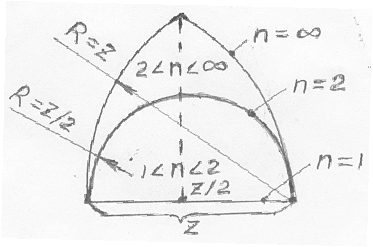
Рисунок1
Из рис. 1 следует, что любая (•) в плоскости чертежа, заключенная между
кривыми, которые соответствуют значениям n=1 и n=![]() ; является вершиной
; является вершиной ![]() , соответствующего решению
уравнения xⁿ+уⁿ=zⁿ при определенном значении 1<n <
, соответствующего решению
уравнения xⁿ+уⁿ=zⁿ при определенном значении 1<n <![]() и z - const. Так как
значение z мы можем выбирать произвольно в
интервале 0<z<
и z - const. Так как
значение z мы можем выбирать произвольно в
интервале 0<z<![]() , то это свидетельствует о
справедливости нашего утверждения, что любой
, то это свидетельствует о
справедливости нашего утверждения, что любой
![]() (кроме
(кроме ![]() со сторонами 1;1;1;?)
является графическим изображением решения уравнения xⁿ+уⁿ=zⁿ в
интервале значений 1<n<
со сторонами 1;1;1;?)
является графическим изображением решения уравнения xⁿ+уⁿ=zⁿ в
интервале значений 1<n<![]() .
.
Однако, вопрос о том, каким значениям n
соответствуют целочисленные (конечные) по х;у;z; решения,
остается открытым. Для его решения построим аналогичные кривые при фиксированном
(const) значении x.
Для краткости приведу сразу его обобщенный рисунок: *
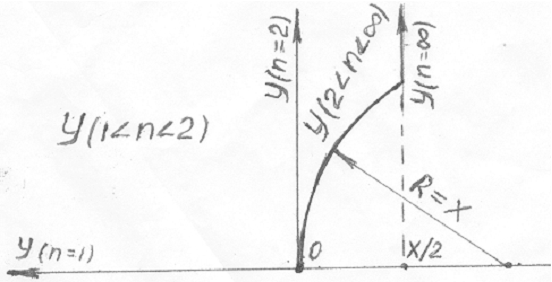
Рисунок 2
Рассмотрев рис.1
и рис.2,
можно сделать вывод, что выбранные нами «критические» кривые, соответствующие
значениям n=1; n=2; n=![]() ; являются не только «кривыми» (так
как они могут быть и прямыми), на которых лежат вершины целочисленных
(конечных) по х; у; z;
; являются не только «кривыми» (так
как они могут быть и прямыми), на которых лежат вершины целочисленных
(конечных) по х; у; z; ![]() , но и являются также
единственными «кривыми» при 1<n<
, но и являются также
единственными «кривыми» при 1<n<![]() , у которых на каждом отрезке
кривизна постоянна (const). То есть,
эти кривые являются либо отрезком прямой, либо частью окружности, либо их
комбинацией. Для всех остальных значений n≠1; 2;
, у которых на каждом отрезке
кривизна постоянна (const). То есть,
эти кривые являются либо отрезком прямой, либо частью окружности, либо их
комбинацией. Для всех остальных значений n≠1; 2;![]() ; эти кривые являются кривыми с
переменной кривизной. Отсюда логично предположить, что все остальные
целочисленные (конечные) по х; у; z; решения
уравнения xⁿ+уⁿ=zⁿ (при 1<
n <
; эти кривые являются кривыми с
переменной кривизной. Отсюда логично предположить, что все остальные
целочисленные (конечные) по х; у; z; решения
уравнения xⁿ+уⁿ=zⁿ (при 1<
n <![]() ) принадлежат уравнениям с n=Б
(учитывая, что 2xⁿ=zⁿ принадлежат n=Б). Подведем
под это логическое предположение математическую базу. Для этого нам необходимо
найти такое геометрическое и соответствующее ему математическое решение,
которое, будучи справедливым при любом 1<n<
) принадлежат уравнениям с n=Б
(учитывая, что 2xⁿ=zⁿ принадлежат n=Б). Подведем
под это логическое предположение математическую базу. Для этого нам необходимо
найти такое геометрическое и соответствующее ему математическое решение,
которое, будучи справедливым при любом 1<n<![]() , позволяло бы вычислить все
возможные целочисленные решения уравнения
, позволяло бы вычислить все
возможные целочисленные решения уравнения ![]() и не позволяло бы x; y; z; принимать
целочисленные (конечные) значения при
и не позволяло бы x; y; z; принимать
целочисленные (конечные) значения при 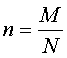 , где М, N – целые положительные числа. Причём, М
> N, то есть,
n > 1 (
, где М, N – целые положительные числа. Причём, М
> N, то есть,
n > 1 (![]() может быть и целым числом). Таким решением является следующее:
может быть и целым числом). Таким решением является следующее:
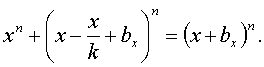
Рассмотрим данное решение на примере ![]() (n = 2). Возьмем
график функции f(
(n = 2). Возьмем
график функции f(![]() ). Выберем на ней произвольную целочисленную по
оси х (•) х. От (•) х откладываем (в
сторону уменьшения) целочисленный отрезок <х, составляющий некоторую часть k от х. Получаем другую
(•) с целочисленной координатой (так как если из целого вычесть целое, то
получается целое). Данную (•) соединяем с (•) графика
). Выберем на ней произвольную целочисленную по
оси х (•) х. От (•) х откладываем (в
сторону уменьшения) целочисленный отрезок <х, составляющий некоторую часть k от х. Получаем другую
(•) с целочисленной координатой (так как если из целого вычесть целое, то
получается целое). Данную (•) соединяем с (•) графика ![]() , соответствующей координатам (х;
, соответствующей координатам (х;![]() ). Получаем отрезок прямой с координатами его концов
). Получаем отрезок прямой с координатами его концов 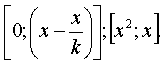 . Переместим данный отрезок, сохраняя его параллельность
первоначальному положению, до совмещения его концов с точками на графике
. Переместим данный отрезок, сохраняя его параллельность
первоначальному положению, до совмещения его концов с точками на графике ![]() . Получим две точки с координатами по оси х, равными у и z, которые и будут
являться решением уравнения
. Получим две точки с координатами по оси х, равными у и z, которые и будут
являться решением уравнения ![]() (см. рис. 3)
(см. рис. 3)
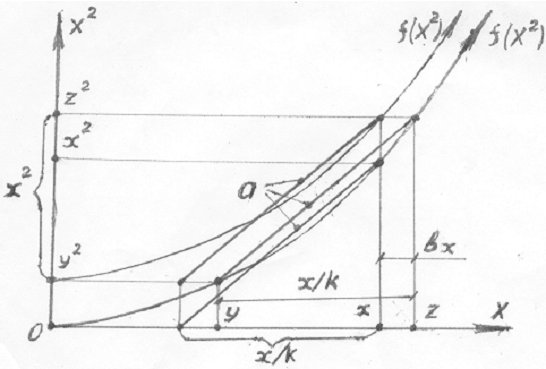
Рисунок 3
В данном случае мы замещаем отрезок графика ![]() отрезком
прямой а, и получается, что сумма
отрезка графика
отрезком
прямой а, и получается, что сумма
отрезка графика ![]() и отрезка графика
и отрезка графика ![]() =а равна
отрезку графика
=а равна
отрезку графика ![]() , где
, где ![]() - необходимое для данного построения смещение отрезка а вдоль оси х. Отсюда:
- необходимое для данного построения смещение отрезка а вдоль оси х. Отсюда: 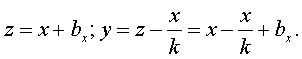
А формула![]() принимает вид:
принимает вид: 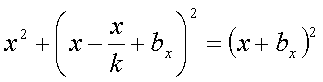 .
.
Данное построение справедливо для всех n > 1.
Критические случаи (n=1; n=![]() ) рассмотрим отдельно*. Таким
образом, от трех переменных х; у; z; мы
перешли к переменным х; k;
) рассмотрим отдельно*. Таким
образом, от трех переменных х; у; z; мы
перешли к переменным х; k; ![]() ; при n=2 (const). А
условие целочисленности x; y; z; обеспечивается
целочисленностью x;
; при n=2 (const). А
условие целочисленности x; y; z; обеспечивается
целочисленностью x; ![]() ;
; ![]() . Следовательно, нам нужно установить, при каких
целочисленных значениях х
значения
. Следовательно, нам нужно установить, при каких
целочисленных значениях х
значения ![]() и
и ![]() одновременно могут принимать целочисленные значения в квадратном уравнении
(n = 2). Для
понимания всех последующих рассуждений и вопроса в целом, необходимо для себя
(самостоятельно) уяснить основные моменты, которые в дальнейшем изложении будут
только подразумеваться.
одновременно могут принимать целочисленные значения в квадратном уравнении
(n = 2). Для
понимания всех последующих рассуждений и вопроса в целом, необходимо для себя
(самостоятельно) уяснить основные моменты, которые в дальнейшем изложении будут
только подразумеваться.
1). Так как уравнение xⁿ+уⁿ=zⁿ нельзя
решать для всех n одновременно, мы решаем его (с
учетом целочисленности х; у; z;) только для n=2 (или любого
другого значения n>1). Таким образом, мы убираем
одну переменную n.
2). Чем больше целочисленное значение х, тем больше значений k, приводящих
к целочисленному значению ![]() . Например: при х=3,
. Например: при х=3, ![]() может = 1;2;
может = 1;2;
а при х=4, ![]() =1; 2; 3;
=1; 2; 3;
Следовательно, возможные значения k
при х=3 это 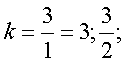
при 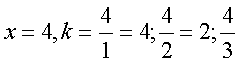 .
.
Таким образом, k может быть либо целым числом,
либо простой дробью ![]() >1. Именно >1,
так как k=1 приводит
значение у к равенству 0. При k<1 построение
невозможно.
>1. Именно >1,
так как k=1 приводит
значение у к равенству 0. При k<1 построение
невозможно.
3). Учитывая второй пункт, а также то, что при любом значении х каждому
значению k соответствует свое строго
определенное значение![]() , следовало бы обозначить
, следовало бы обозначить ![]() через
через
![]() (
(![]() от k).
Но для упрощения записи будем писать
от k).
Но для упрощения записи будем писать ![]() , помня о вышесказанном, так как
, помня о вышесказанном, так как ![]() мы можем определить,
только задав
мы можем определить,
только задав
значения х; k.
4). Имея же целью вычислить взаимосвязь х и ![]() при каждом конкретном
значении k мы получаем: при k - const,
при каждом конкретном
значении k мы получаем: при k - const, ![]() , где
, где ![]() : - смещение при данном k и х = 1. Это подтверждается следующими
выкладками. Возьмем уравнение
: - смещение при данном k и х = 1. Это подтверждается следующими
выкладками. Возьмем уравнение 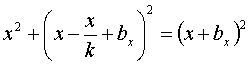 и придадим х значение = 1, получим:
и придадим х значение = 1, получим:
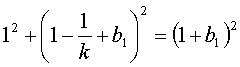 .
.
Разделив уравнение 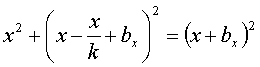 на
на ![]() , получим:
, получим:
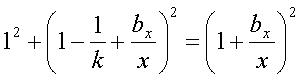 .
.
Сравнив оба результата, получим 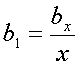 или
или![]() .
.
5). При этом, учитывая первый
пункт, необходимо помнить, что всё последующее (второй, третий и четвертый
пункты) справедливо при всех 1 < n
< ![]() (целых, дробных и
(целых, дробных и ![]() дробных периодических и непериодических значениях
n).
дробных периодических и непериодических значениях
n).
Теперь, с учетом всего
вышесказанного, приступим к нахождению всех
возможных целочисленных решений уравнения ![]() . Итак, от одной переменной (n) мы
избавились. Теперь (временно) уберем из рассмотрения вторую (х). Для этого
установим взаимосвязь между
. Итак, от одной переменной (n) мы
избавились. Теперь (временно) уберем из рассмотрения вторую (х). Для этого
установим взаимосвязь между ![]() и k
при х=1, то есть, между
и k
при х=1, то есть, между ![]() и k. Тогда
уравнение
и k. Тогда
уравнение 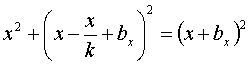 принимает вид:
принимает вид:
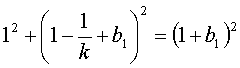 или
или 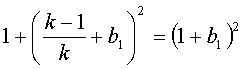 ;
;
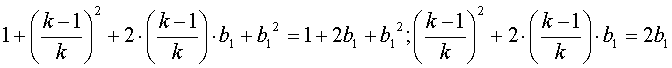 ;
;
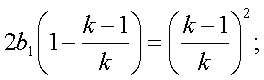
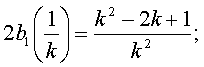
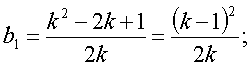 *
*
Но так как мы ищем целочисленные решения уравнения ![]() необходимо, чтобы
необходимо, чтобы ![]() равнялось целому
числу. Но
равнялось целому
числу. Но ![]() и поэтому для целочисленности
и поэтому для целочисленности ![]() , необходимо, чтобы х=2k
(пока с
учетом целочисленности k). Тогда
, необходимо, чтобы х=2k
(пока с
учетом целочисленности k). Тогда ![]() . Подставив эти значения х и
. Подставив эти значения х и ![]() в уравнение
в уравнение 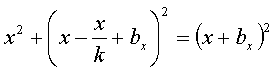 , получим:
, получим:
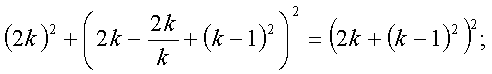
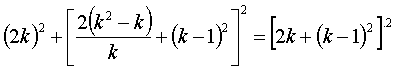 ;
;
![]() ;
;
![]()
![]() .*
.*
Так как![]() ,
,
мы получаем тождество, позволяющее вычислять целочисленные по х; у; z; решения
уравнения ![]() при целочисленных
значениях k. Но k может
принимать и любое дробное > 1
значение =
при целочисленных
значениях k. Но k может
принимать и любое дробное > 1
значение = ![]() . Как в этом случае изменится формула
. Как в этом случае изменится формула ![]() ?
?
Она примет вид: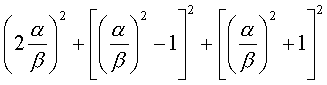 .
.
Умножив на ![]() получим:
получим:![]() , где
, где ![]() - целые положительные числа, причём,
- целые положительные числа, причём, ![]() так как k > 1. Данная
формула, так же являясь тождеством, позволяет вычислить все
целочисленные по х; у; z; решения уравнения
так как k > 1. Данная
формула, так же являясь тождеством, позволяет вычислить все
целочисленные по х; у; z; решения уравнения
![]() . Решая уравнение
. Решая уравнение 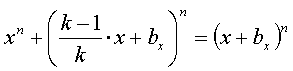 по вх при любом конкретном значении n > 1, мы
всегда будем получать уравнение на порядок ниже (n-1) степени. И
только квадратное уравнение превращается в линейное (2–1=1), что и позволяет ему иметь
целочисленные по х;у;z; решения.
по вх при любом конкретном значении n > 1, мы
всегда будем получать уравнение на порядок ниже (n-1) степени. И
только квадратное уравнение превращается в линейное (2–1=1), что и позволяет ему иметь
целочисленные по х;у;z; решения.
Таким образом, 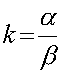 и
и 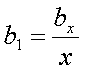 при всех 1<n≠2
связаны зависимостью (либо k, либо
при всех 1<n≠2
связаны зависимостью (либо k, либо 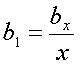 равняются Б), но
равняются Б), но 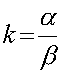 может равняться любому
конечному значению равному n (в этом случае
отрезок перемещаемой прямой является отрезком касательной)*. Тогда получаем,
что либо n, либо
может равняться любому
конечному значению равному n (в этом случае
отрезок перемещаемой прямой является отрезком касательной)*. Тогда получаем,
что либо n, либо 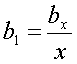 равняется Б. Но для целочисленности х; у; z; ни k, ни
равняется Б. Но для целочисленности х; у; z; ни k, ни 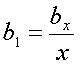 не должны равняться Б. Следовательно, k ≠ n = Б (либо
не должны равняться Б. Следовательно, k ≠ n = Б (либо ![]() ). Таким образом, решение
поставленной нами задачи (определить значения n, при
которых возможны целочисленные по х;у;z; решения уравнения xⁿ+уⁿ=zⁿ) можно
сформулировать следующим образом:
). Таким образом, решение
поставленной нами задачи (определить значения n, при
которых возможны целочисленные по х;у;z; решения уравнения xⁿ+уⁿ=zⁿ) можно
сформулировать следующим образом:
1). Уравнение вида xⁿ+уⁿ=zⁿ, где n>1 может
иметь целочисленные (конечные) по х; у; z; решения
только при n = 2; во всех
остальных случаях целочисленность (конечность) х; у; z; приводит
значение n к равенству Б, либо ![]() . Целочисленность
х;у;z; в уравнении
второго порядка (n=2) возможна
только при условии, что х; у; z; являются
числами, определяемыми по формулам:
. Целочисленность
х;у;z; в уравнении
второго порядка (n=2) возможна
только при условии, что х; у; z; являются
числами, определяемыми по формулам: ![]() где
где ![]() - целые положительные числа, причем
- целые положительные числа, причем ![]() .
.
Формулировку данного решения можно записать и так: уравнение ![]() ; являясь уравнением четырех переменных (х; у; z; n) в
интервале значений
; являясь уравнением четырех переменных (х; у; z; n) в
интервале значений ![]() ; может иметь целочисленные по всем четырем переменным
решения, только при n=1 и n=2.
Во всех остальных случаях целочисленность
(конечность) любых трех переменных приводит значение четвертой к равенству Б; или
; может иметь целочисленные по всем четырем переменным
решения, только при n=1 и n=2.
Во всех остальных случаях целочисленность
(конечность) любых трех переменных приводит значение четвертой к равенству Б; или ![]() .
.
2). Уравнение ![]() , в интервале значений n>1, справедливо
при всех целых (конечных) значениях n, кроме n=2, и любом а – целом или дробном.
, в интервале значений n>1, справедливо
при всех целых (конечных) значениях n, кроме n=2, и любом а – целом или дробном.
При n =2 оно справедливо
только при условии, что а≠ отношению любых двух из трех чисел, определяемых по
формулам:
![]() , где
, где ![]() - целые положительные
числа, причем
- целые положительные
числа, причем ![]() .
.
Причем из того, что уравнение ![]()
![]() ; справедливо при всех а=с ( с – целое число), а для нахождения
целочисленных по х;
у; z
решений уравнения
; справедливо при всех а=с ( с – целое число), а для нахождения
целочисленных по х;
у; z
решений уравнения ![]() , значение а должно
равняться отношению двух из трех чисел (х; у; z), определяемых
по вышеприведенным формулам.
, значение а должно
равняться отношению двух из трех чисел (х; у; z), определяемых
по вышеприведенным формулам.
Отсюда следует, что отношения 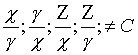
Таким образом, мы получаем
«системы» уравнений, не имеющих целочисленных решений:
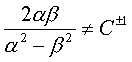 ;
; 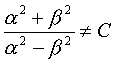 ;
; 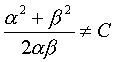 .
.
Некоторые и из этих уравнений,
записанные в частном виде (при определенном значении С), рассматриваются в теории чисел на предмет их целочисленного
решения. Например, ![]() ; или
; или ![]() ; что равноценно
; что равноценно 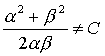 ; при С=1 и С=2.
; при С=1 и С=2.![]() Записи этих уравнений в общем виде я не нашел.
Записи этих уравнений в общем виде я не нашел.
Знак ![]() в «формулах общего
вида» означает, что эти уравнения не могут иметь целочисленных решений при условии,
что
в «формулах общего
вида» означает, что эти уравнения не могут иметь целочисленных решений при условии,
что ![]() .
.
P.S. Тот факт,
что нахождение целочисленных решений квадратного уравнения
![]() более полно
описывается через несколько переменных
(
более полно
описывается через несколько переменных
(![]() ;
; ![]() ), чем через одну (К)*,
позволяет предположить, что описать простые числа (
), чем через одну (К)*,
позволяет предположить, что описать простые числа (![]() ) можно проще и полнее через несколько переменных, а не через
одну (являющуюся одновременно номером числа в ряду простых чисел (
) можно проще и полнее через несколько переменных, а не через
одну (являющуюся одновременно номером числа в ряду простых чисел (![]() )), как это принято в теории чисел.*
)), как это принято в теории чисел.*
Причем простые числа (![]() ) проще описывать не через равенство (=), а через неравенство (
) проще описывать не через равенство (=), а через неравенство (![]() ) как это сделано в «формулах общего вида». Т.е. мы описываем
сложные числа (
) как это сделано в «формулах общего вида». Т.е. мы описываем
сложные числа (![]() ) через равенство (=)
и, заменяя его на неравенство (
) через равенство (=)
и, заменяя его на неравенство (![]() ), исключаем сложные числа (
), исключаем сложные числа (![]() ) и оставляем простые (
) и оставляем простые (![]() ).
).
Вот как это выглядит в математической записи:
Все простые числа (![]() ) кроме числа «2» находятся в ряду нечетных чисел (
) кроме числа «2» находятся в ряду нечетных чисел (![]() ), которые можно описать через их номер в ряду нечетных чисел
(n)
формулой
), которые можно описать через их номер в ряду нечетных чисел
(n)
формулой
![]()
Число «2» хоть и находится в ряду четных чисел, является простым по
определению. Ведь четные числа – это числа, которые делятся на «2». Но для
числа «2» это означает, что оно делится на «1» и само на себя (на 2).
Можно показать, что нечетное число (![]() ) является сложным (
) является сложным (![]() ), если его номер числа в ряду нечетных чисел (n) равняется 2ab+a+b+1.
), если его номер числа в ряду нечетных чисел (n) равняется 2ab+a+b+1.
Соответственно, если номер числа в ряду нечетных чисел ![]() , это число является простым (
, это число является простым (![]() ).
).